前言

从人类开始认识数字的那一刻起，计算就成为了一个核心的问题。最初，人们通过数数和用手指头计算来解决简单的数学问题。随着时间的推移，人类发明了算筹和算盘，不断改进他们的计算方法。这一切的目的都是为了解决一个问题：如何准确快速地计算出数学公式的结果。随着数学的不断发展，算式变得越来越复杂，从简单的加减法到涉及平方、开方甚至指数运算的公式。为了应对越来越复杂的计算需求，机械计算器应时而生。这些基于机械结构的设备能够执行各种计算任务，将数学计算与物理机械巧妙结合。¹随着电子技术的发展，计算机技术迎来了革命性的进步，使得计算过程大幅度提速并且更加准确。
PS：在此篇不区分计算机和计算器，它们一律都是能完成数学计算的机器。

计算和电力

电力的发展，给我们带来了改进计算机的机会。我们现在有个开关，能够控制电路的通断。问题是这和计算有什么关系呢？灯是否亮起来与计算有关吗？²

计算的本质是加法

我们先从最简单的加减乘除开始。四则运算的实质可以归类到一种，也就是加法。在这里我们引入负数的概念。
其中：

1. 减法可以视为加上一个负数的操作。例如，$(5 - 3) $可以理解为$ (5 + (-3))$。

2. 乘法可以看作是重复加法。比如，$(4 \times 3)$ 可以看作是$ (4 + 4 + 4)$。

3. 除法则可以视为乘以一个分数（或乘以一个数的倒数）。例如$(8 \div 4) $可以理解为$ (8 \times \frac{1}{4})$。

将四则运算简化为加法和乘以特定数的思想是一种有用的数学抽象。所以，我们在制作计算机的时候，可以对计算过程进行简化。也就是只用一种运算符$+$，那么，我们如何获得一个使用电力的加法器呢？能做$1+1=2$的那种。

电信号的本质是通断

电信号的传输可以简单地理解为通过改变电流或电压的方式来携带和传递信息。在数字通信系统中，这种信号通常表现为两种状态：高电压和低电压，这对应于二进制的1和0。

想象一下，每一个开关都代表一个电信号的状态。当开关关闭时，它可能代表0（低电压），当开关打开时，它代表1（高电压）。这种方式非常适合电脑系统和其他数字设备，因为它们就是基于这些基本的开（1）和关（0）的操作来处理和存储信息。

在进行二进制加法时，我们就是在操作这些开关。比如，两个开关都是关（0+0），结果还是关（0）。一个开（1），一个关（0），结果是开（1）。两个开关都是开（1+1），根据二进制的规则，这时会进位，变成10（在十进制中表示为2）。这就像是小学数学里的进位加法，只不过我们是在用开关来表示数字。

所以，我们先不急着奢求十进制内的加减法。既然手头已经可以简单的掌握电路的通断，那么就可以试一试能不能在二进制内做文章了。刚好，现在有一类电路，称之为门电路，可以满足我们的操作。

门电路

门电路是一系列电路的统称，用于执行简单的逻辑操作，如“与”、“或”和“非”。这些操作决定了电路的输出信号，基于其输入信号是否为高（1）或低（0）。这些电路是构建复杂电子系统的基础。

二进制和逻辑运算

但先别急，我们需要把逻辑操作和二进制的关系理清楚才能利用这一类电路啊。对于二进制的操作，我们用最简单的加法为例。
0+0＝0
0+1＝1
1+0＝1
1+1＝10
同样的，我们把熟悉的形式逻辑运算符放上来。
形式逻辑使用一套标准的符号来精确地表示逻辑表达式。这些符号包括：

1. 命题符号：通常用大写字母 $(P, Q, R) $等表示不同的命题。

2. 逻辑连接词：

   • 非（Negation）：$(\neg) $或 $(\sim)$，表示逻辑“非”或“不是”。
   • 合取（Conjunction）：$(\wedge)$，表示逻辑“与”。
   • 析取（Disjunction）：$(\vee)$，表示逻辑“或”。
   • 蕴含（Implication）：$(\rightarrow)$ 或$ (\supset)$，表示逻辑“如果…那么…”。
   • 等价（Biconditional）：$(\leftrightarrow)$ 或 $(\equiv)$，表示逻辑“当且仅当”。

3. 量词：

   • 全称量词（Universal quantifier）：$(\forall)$，表示“对所有”。
   • 存在量词（Existential quantifier）：$(\exists)$，表示“存在”。

4. 括号：用来明确运算的优先顺序，常见为圆括号$ (())$。

所以，是不是看出来一些东西了？
二进制加法在某种程度上与形式逻辑的析取（逻辑“或”）操作有相似之处，尤其是在不考虑进位的情况下。我们可以使用逻辑符号来表示二进制加法中的一些基本操作，特别是在处理单个位的加法时。

二进制加法的基本规则如下：

• $(0 + 0 = 0)$
• $(0 + 1 = 1)$
• $(1 + 0 = 1)$
• $(1 + 1 = 10)$（考虑进位的情况）

在不考虑进位的情况下，$(1 + 1 = 1)$。这和逻辑的析取（或）操作很相似，其中：

• $(\text{false} \vee \text{false} = \text{false})$（0 或 0 = 0）
• $(\text{false} \vee \text{true} = \text{true})$（0 或 1 = 1）
• $(\text{true} \vee \text{false} = \text{true})$（1 或 0 = 1）
• $(\text{true} \vee \text{true} = \text{true})$（1 或 1 = 1）

因此，在不考虑进位的情况下，二进制加法可以用逻辑的析取（或）操作来描述。这说明虽然二进制加法和形式逻辑不是同一回事，但逻辑运算符可以用来模拟某些简单的数学运算。如果要表示完整的二进制加法，还需要考虑其他逻辑操作和结构（如逻辑与来处理进位）。

回到门电路的定义，我们发现可以利用门电路把二进制和逻辑操作联系在一起。这一点是实现后续所有计算的基础。换句话说，电路并没有直接的0和1，而是人类定义的0和1。同样的，逻辑也没有实体，但是可以利用开关的通断来表达逻辑关系。所以，我们在语言中的逻辑推理和数学运算将可以在物理的载体上实现，这就是引入门电路的意义。

基本门电路

同样的，不考虑赋值等进阶情况，我们只考虑逻辑运算，是不是可以得到三种关系符号？与、或、非
那么，门电路中也有与门、或门、非门执行基本的逻辑运算，这些逻辑运算是计算机处理二进制信息的基础。下面是如何进一步将二进制和逻辑运算通过门电路联系起来的简要说明：

1. 与门（AND Gate）：

   • 逻辑运算：只有当所有输入都为1时，输出才为1。
   • 二进制示例：$(1 \text{ AND } 1 = 1)$, $(1 \text{ AND } 0 = 0)$,$(0 \text{ AND } 0 = 0)$
   • 电路符号：通常表示为一个D形图形，输入线进入平面一侧，输出线从尖端出来。

2. 或门（OR Gate）：

   • 逻辑运算：只要有一个输入为1，输出就为1。
   • 二进制示例：$(1 \text{ OR } 1 = 1)$, $(1 \text{ OR } 0 = 1)$, $(0 \text{ OR } 0 = 0)$
   • 电路符号：其符号与与门类似，但更为弯曲，表明它具有更包容的逻辑性质。

3. 非门（NOT Gate）：

   • 逻辑运算：输入的反向值作为输出。
   • 二进制示例：$(\text{NOT } 1 = 0)$, $(\text{NOT } 0 = 1)$
   • 电路符号：通常是一个三角形，带有一个圆圈在尖端，表示输出是输入的反转。

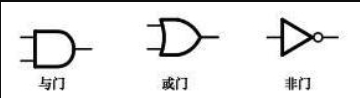
通过这些基本的门电路，我们可以构建更复杂的逻辑电路，实现更复杂的二进制运算。在实际的应用中，组合这些基本门电路可以设计出实现特定逻辑功能的电路系统，比如加法器、计数器、寄存器等。

【如果只是为了理解现代电子计算机的本质，其实到这里基本上讲完了，后面是进一步延伸。想要跳到LLM的可以直接过去了。】

---

进阶门电路

众所周知，人类很喜欢排列组合，那么把上面三种门电路两两结合就会得到什么呢？
将三种基本逻辑门（与门、或门、非门）两两结合，我们可以得到一些更复杂的逻辑运算，如下所示：

1. 与非门 (NAND gate)

   • 逻辑运算：与运算的反运算，即 NOT (A AND B)
   • 二进制示例：如果 A=1, B=1，则输出为 0；如果 A=1, B=0 或 A=0, B=1 或 A=0, B=0，则输出为 1。
   • 电路符号：与门的符号，但输出端有一个小圆圈。
   • 输入输出个数：两个输入，一个输出。

2. 或非门 (NOR gate)

   • 逻辑运算：或运算的反运算，即 NOT (A OR B)
   • 二进制示例：如果 A=0, B=0，则输出为 1；如果 A=1, B=0 或 A=0, B=1 或 A=1, B=1，则输出为 0。
   • 电路符号：或门的符号，但输出端有一个小圆圈。
   • 输入输出个数：两个输入，一个输出。

3. 异或门 (XOR gate)

   • 逻辑运算：相当于 “或” 和 “与非” 的组合，即 (A AND NOT B) OR (NOT A AND B)
   • 二进制示例：如果 A=1, B=0 或 A=0, B=1，则输出为 1；如果 A=1, B=1 或 A=0, B=0，则输出为 0。
   • 电路符号：类似或门的符号，但在输入端多一个弧线。
   • 输入输出个数：两个输入，一个输出。

4. 同或门 (XNOR gate)

   • 逻辑运算：异或运算的反运算，即 NOT (A XOR B)
   • 二进制示例：如果 A=1, B=1 或 A=0, B=0，则输出为 1；如果 A=1, B=0 或 A=0, B=1，则输出为 0。
   • 电路符号：异或门的符号，但输出端有一个小圆圈。
   • 输入输出个数：两个输入，一个输出。

这些门通过结合基本逻辑门的特性，实现了更为复杂的逻辑功能。
下面是对应的符号图。

真值表

是不是已经开始脑子混乱了，到底什么门会出现什么功能，或者什么样的输入会出现什么样的输出呢？这个时候就要一个真值表了。
真值表是一种用来描述逻辑门或布尔表达式是如何工作的工具。它列出了所有可能的输入组合，以及对应的输出结果。这就像是一个查找表，你可以通过查看输入的值来找到输出应该是什么。真值表帮助我们理解在不同输入情况下，一个逻辑电路或一个数学表达式会如何反应。
刚刚我们学会了AND、OR、NOT、NAND、NOR、XOR和XNOR门。这些门通过接收二进制输入（0或1），根据特定的逻辑关系产生一个输出。下面是这七种逻辑门的真值表：

1. AND门 (与门)：

   • 输入: 两个或以上
   • 逻辑: 所有输入均为1时，输出为1；否则为0。

   A	B	Output
   0	0	0
   0	1	0
   1	0	0
   1	1	1

2. OR门 (或门)：

   • 输入: 两个或以上
   • 逻辑: 至少有一个输入为1时，输出为1；否则为0。

   A	B	Output
   0	0	0
   0	1	1
   1	0	1
   1	1	1

3. NOT门 (非门)：

   • 输入: 一个
   • 逻辑: 输入为0时输出为1，输入为1时输出为0。

   A	Output
   0	1
   1	0

4. NAND门 (与非门)：

   • 输入: 两个或以上
   • 逻辑: 与AND相反，只有当所有输入都为1时，输出为0；其他情况输出为1。

   A	B	Output
   0	0	1
   0	1	1
   1	0	1
   1	1	0

5. NOR门 (或非门)：

   • 输入: 两个或以上
   • 逻辑: 与OR相反，只有当所有输入都为0时，输出为1；其他情况输出为0。

   A	B	Output
   0	0	1
   0	1	0
   1	0	0
   1	1	0

6. XOR门 (异或门)：

   • 输入: 两个
   • 逻辑: 输入不同时输出为1，相同时输出为0。

   A	B	Output
   0	0	0
   0	1	1
   1	0	1
   1	1	0

7. XNOR门 (同或门)：

   • 输入: 两个
   • 逻辑: 与XOR相反，输入相同时输出为1，不同时输出为0。

   A	B	Output
   0	0	1
   0	1	0
   1	0	0
   1	1	1

这些真值表提供了各逻辑门在不同输入下的输出结果，是电子和计算机科学中的基本工具。

关于这部分内容，我不希望死记硬背，而是去理解这背后的深层关系。同时如果实在是记不住就记不住吧，原理就是这样后面慢慢拼凑也行。就和前三种门是后四种门的基础，那么我们利用这七种门可以干啥呢？继续造计算机呀~³

不能进位的门电路计算机

说真的，大家都不能一步登天，所以从最简单的加法和不需要进位开始学习吧。
相当于小孩子学习十以内的加法
二进制加法中
0+0＝0
0+1＝1
1+0＝1
这三种情况是不需要进位的，我们来仔细看看，是不是和或门的真值表前三行一样？
OR门 (或门)：

• 输入: 两个或以上

• 逻辑: 至少有一个输入为1时，输出为1；否则为0。

  A	B	Output
  0	0	0
  0	1	1
  1	0	1

好啦，我们现在就用或门造了个最简单不能进位的计算机。

能进一位的门电路计算机

这个时候就要想办法来解决1+1=10的问题了。
好的，让我们用最简单的方式来解释这个问题。1+1=10这个式子，实际上是在二进制（即计算机语言）中的表达方式。在我们常用的十进制系统中，1+1等于2。但在二进制系统中，数字“2”被写作“10”。

使用逻辑门实现1+1=10

要解决1+1=10这个问题，我们主要用到的是“XOR逻辑门”和“AND逻辑门”。

1. XOR逻辑门（异或门）：当两个输入不相同时，输出为1；当两个输入相同时，输出为0。

   • 输入：1, 1
   • 输出：0 （因为两个输入相同）

2. AND逻辑门（与门）：只有当两个输入都为1时，输出才为1。

   • 输入：1, 1
   • 输出：1 （因为两个输入都是1）

结合这两个逻辑门

在1+1的计算中，我们把两个数字输入到XOR逻辑门和AND逻辑门中。

• XOR门的输出将成为结果的低位（二进制中的“个位”）。
• AND门的输出将成为结果的高位（二进制中的“十位”）。

所以，对于输入1和1：

• XOR门输出0（因为输入相同）
• AND门输出1（因为两个输入都是1）

最终，输出是10（在二进制中表示2）。

这样，通过简单的逻辑门电路，我们就实现了“1+1=10”的运算！

原理分析

使用XOR逻辑门和AND逻辑门来实现二进制加法是因为这两种门能够很好地处理二进制数位的加法规则，特别是处理进位情况。让我们一步步分解来看：

二进制加法的基本规则

1. 0 + 0 = 0：无进位
2. 1 + 0 = 1 或 0 + 1 = 1：无进位
3. 1 + 1 = 10：结果是0，并且有一个进位到下一高位

XOR 逻辑门（异或门）

XOR逻辑门输出在两个输入位不同时为1，相同时为0。这正好符合二进制加法中的加和（不考虑进位）：

• 0 XOR 0 = 0
• 1 XOR 0 = 1
• 0 XOR 1 = 1
• 1 XOR 1 = 0（这里虽然实际应有进位，但XOR逻辑门只负责结果的本位）

AND 逻辑门（与门）

AND逻辑门只有在两个输入位都为1时输出1，这恰好用来处理进位的情况：

• 0 AND 0 = 0
• 1 AND 0 = 0
• 0 AND 1 = 0
• 1 AND 1 = 1（产生一个进位到下一高位）

结合XOR和AND门

• XOR门的输出提供了两个位相加时的基本结果（不含进位）。
• AND门的输出提供了是否需要向更高位进位的信息。

这种门的组合可以扩展到更复杂的二进制全加器中，其中还需要用到OR逻辑门来合并来自低位的进位输入和当前位的进位输出。

总之，XOR和AND逻辑门是构建二进制加法电路的基础，因为它们能够简单有效地模拟二进制加法的行为，特别是在处理进位方面非常关键。

篇中整理

1. 计算的根本是加法，所以先从加法开始推理，剩下其他运算都可以转换为加法。
2. 我们可以通过控制电路通断的方式来代表逻辑状态，进而和前面的加法结合。
3. 虽然我们日常用十进制，但是现在还是先不把机器弄的太复杂，二进制的两种状态已经够折磨人了。
4. 将二进制的规律和门电路的真值表对应，就知道对应的计算机怎么制作了（起码有思路）。换句话说就是用电路的输入输出实现二进制的计算过程。

半加器

半加器：半加器是一种电路，它可以处理两个二进制数的加法，但是不考虑来自低位的进位输入。它只能处理最基本的加法，比如 $(1 + 1)$ 或$ (0 + 1)$。它会输出一个和位（Sum）和一个进位位（Carry），其中和位表示结果的低位，进位位在结果比一位还要高的位置上使用（比如 $(1 + 1 = 10) $中的 '1' 就是进位）。
所以，我们刚刚误打误撞搓出来的能进一位的门电路计算机就是半加器，但是我让AI用人话再说了一遍。
半加器是全加器的简化版，它只处理两个输入位的加法，而不考虑之前的进位。想象一下你有两个盒子（分别代表A和B），每个盒子里可以放一个球（球代表1）或者不放球（代表0）。现在我们要把这两个盒子里的球数加起来，但这次我们不用担心之前有没有球（进位）留在场上。

步骤和用到的工具

1. 异或门（XOR）：这是一个特别的计数器。如果A盒子和B盒子里球的数量是奇数（即一个有球，一个没球），它就会显示1（即球的总数是1），代表我们的和位（Sum）。如果两个盒子要么都有球，要么都没球，它就显示0。

2. 与门（AND）：这是一个严格的检查员，只有当A盒子和B盒子里都有球时，它才表示有进位（Cout）。这是因为两个球加在一起，需要一个新的盒子来放多出来的球。

逻辑变换

• 和（Sum）：使用异或门来计算A和B盒子里球的总数，而不考虑任何之前的进位。这是因为半加器本身不处理进位输入，所以我们只关心当前两个盒子里的球。

• 进位输出（Cout）：用与门检查A和B盒子，如果两个盒子都有球，那就表示需要一个新的盒子来存放多出来的球，即产生了进位。

结论

半加器就像是我们的玩具游戏的一个简单环节，它只考虑两个盒子的球，帮助我们计算这两个盒子能放多少球，并告诉我们是否需要另一个盒子来放多的球。这个设计简单但非常有用，尤其是在我们不需要担心之前的进位时。它是构建更复杂加法机器（如全加器）的基础。

全加器

全加器：全加器是一种更复杂的电路，它不仅处理两个二进制数的加法，还考虑了来自低位的进位输入。这意味着全加器可以连续串联起来，处理多位数的加法。全加器有三个输入：两个加数位和一个低位进位输入，输出仍然是一个和位和一个进位位。
相比于半加器非常基本的加法操作，全加器能够处理更复杂的情况，特别是在进行连续位的加法时。全加器可以视为半加器的扩展，它加入了对进位的处理。
全加器的门电路实现通常涉及多个基本逻辑门，如与门（AND）、或门（OR）、异或门（XOR）。全加器接受三个输入：两个加数（A和B）以及一个来自低位的进位输入（Cin），并产生两个输出：和（Sum）和进位输出（Cout）。
相当于小孩子学到用竖式计算任意的加法。
【可能会弄的很懵，后文会有解释。】

真值表

下表展示了全加器的所有输入组合及其对应的输出：

A	B	Cin	Sum	Cout
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

【这部分可能不是那么好理解，请作为铺垫继续往后看。】

1. A 和 B：这两个是全加器的主要输入，代表你想要相加的两个二进制位。例如，在两个数字 1101 和 1011 相加时，你会一位一位地把这些数字对齐，然后逐位相加，这里的 A 和 B 就是在每一位上进行相加的那两个位。

2. Cin (Carry-in)：这是全加器的第三个输入，代表从前一位加法操作中得到的进位。在做二进制加法时，如果两个位相加超过1（即总和等于2或3），就会产生一个进位值，这个进位值会被加到下一位的计算中。Cin 就是这个进位输入。

3. Sum (和)：这是全加器的一个输出，表示当前位的加法结果。简单来说，就是当前位 A 和 B 相加再加上任何的进位 Cin 后的结果（仅此位的结果，不包括任何产生的进位）。

4. Cout (Carry-out)：这是全加器的另一个输出，表示产生的进位。如果当前位的加法操作产生了进位（即总和大于等于2），这个进位就会通过 Cout 传递到下一位的加法操作中去。

这样的设计使得全加器不仅能处理两个位的简单加法，还能处理因为前一位加法而来的进位，使其能够被串联起来，连续处理多位数字的加法操作。

门电路实现

全加器的门电路可以通过以下逻辑公式来实现：

• Sum = (A XOR B) XOR Cin：和位是两个加数和低位进位的异或结果。
• Cout = (A AND B) OR (B AND Cin) OR (A AND Cin)：进位输出是这三个条件的或运算结果。

在门电路中，我们通常使用两个异或门来生成和位，第一个异或门计算 $(A \oplus B)$，第二个异或门将这个结果与$(C_{in})$异或得到和位。

进位输出$(C_{out})$是通过三个与门和一个或门来实现的，每个与门计算一种进位条件，然后三者的结果通过一个或门合并。

这样的设计确保了全加器能够准确地计算两个二进制数的和，以及正确地向高位传递进位。

全加器中的二进制输出和进位理解

在全加器中，输出结果可以被理解为一个二进制数，其中 Cout（进位输出） 是最高位，而 Sum（和） 是最低位。这就像你在做十进制加法时处理进位一样，只不过这里是在二进制世界中。

让我们用二进制的视角来解释这个概念：

在二进制加法中，加法的规则如下：

• 0 + 0 = 00（没有和，也没有进位）
• 0 + 1 = 01（和是1，没有进位）
• 1 + 0 = 01（和是1，没有进位）
• 1 + 1 = 10（没有和，有一个进位）

现在，如果加法涉及到进位输入（Cin），结果就可能是这样：

• 1 (A) + 1 (B) + 1 (Cin) = 11（和是1，有一个进位）

这里的两个位表示：

• 最低位（右边的位）是 Sum
• 最高位（左边的位）是 Cout

例如，当你计算 $(1 + 1) $时：

• 二进制的输出是 10，这里 0 是 Sum，1 是 Cout。

而当计算 $(1 + 1 + 1)$ （即 A = 1, B = 1, Cin = 1）时：

• 二进制的输出是 11，这里 1 是 Sum，另一个 1 是 Cout。

所以，对于全加器，你可以这样想象：它的输出是一个两位的二进制数，其中 Cout 是这个二进制数的最高位（第二位），Sum 是这个二进制数的最低位（第一位）。这样，全加器不仅计算当前位的加法结果，还提供是否需要进位到下一位的信息。

人话解释

好的，让我们用更简单的方式来解释全加器的工作原理，就像我们在和小猫娘解释玩具是如何运作的一样：

想象一下，你有两个盒子（分别代表A和B），每个盒子里可以放一个球（球代表1）或者不放球（代表0）。现在我们要把这两个盒子里的球数加起来，但我们的游戏有一个特殊规则，就是每个盒子只能放一个球，如果加起来超过一个球，我们就需要把多出来的球放到一个新的盒子里（这个新盒子就是进位Cout）。

步骤和用到的工具

1. 异或门（XOR）：想象它是一个特殊的计数器，它只在你给它奇数个球时显示1（即一个球）。所以，如果盒子A和盒子B里都有球或都没有球，它显示0；如果只有一个盒子有球，它显示1。这就帮我们计算出了没有考虑进位的结果（Sum）。

2. 与门（AND）：这像是一个严格的守门员，只有当两个盒子A和B都有球时，它才开门（输出1）。这告诉我们是否需要把球（进位）放到新的盒子里。

3. 或门（OR）：这是一个宽松的门，只要有任何一个输入有球（即为1），它就开门。我们用这个来决定最终是否有球需要进入到新的进位盒子Cout。比如，如果A和B两个盒子都有球，或者A和之前的进位Cin有球，或者B和Cin有球，我们就把球放到新的进位盒子里。

逻辑变换

• 和（Sum）：我们先用异或门看A和B盒子里的球数，然后再用异或门考虑进位Cin。这就像我们先看A和B，算出一个初步结果，再用这个结果去和前面的进位盒子比较，得到最终的和。

• 进位输出（Cout）：我们用与门检查A和B，然后用或门把所有可能产生的进位情况合并。这就像我们在检查每种可能需要把球放到进位盒子的情况。

结论

这样的玩具设计，让我们可以通过简单的计数和规则检查，把两个盒子里的球数加起来，并且正确处理进位的问题。通过这种方式，我们可以把许多这样的玩具连在一起，来处理更多盒子的加法问题。这就是全加器如何一步步处理我们的“球加法”游戏的逻辑变换。

---

【下面可以不看了，我作为补充添加进来的。】

---

补充例子

全加器就像是一个小巧的算术师，帮助我们处理二进制数字的加法，还要牢记之前是否有额外的1需要加入。设想你在解决一个拼图，每次你都需要将两块拼图片相加，同时还要考虑之前是否留下了一块额外的拼图片。这位算术师使用一些特别的技巧（逻辑门）来帮助你算出这些数字的和以及是否还有额外的1需要传递到下一次计算中。

技巧（逻辑门）介绍

1. 变形术 (异或门 XOR)：这个技巧帮助我们计算两个数字相加的结果，但不包括之前留下的1。它的特点是，当你给它两个数字，只有当这两个数字不相同时（一个是0，一个是1），它才会输出1，否则输出0。

2. 镜像术 (与门 AND)：这个技巧用来检查是否有两个1需要相加。只有当你给它的两个数字都是1时，它才会告诉你“这里有额外的1需要在下一次加上”。

3. 聚集术 (或门 OR)：这个技巧用来处理从不同地方可能出现的1，只要任何一个地方出现了1，它就会告诉你“这里有一个1！”

技巧（逻辑门）公式

• 总和 = 变形术(A和B) 再用变形术(结果和Cin)：
  先使用变形术计算A和B的初步结果，然后再将这个结果与之前留下的1使用变形术计算一次，得到最终的总和。

• 是否还有1要传递 = 镜像术(A和B) 聚集 镜像术(A和Cin) 聚集 镜像术(B和Cin)：
  这个公式检查所有可能会产生额外1的情况，只要任何一个情况成立，就会产生一个新的1在下次计算时使用。

因此，这位小巧的算术师（全加器）通过这些技巧帮助我们把二进制的数字相加，不仅计算出每一位的结果，还记住是否有额外的1需要加到下一位。这样，我们就可以将许多这样的算术师串联起来，依次处理更长的数字串。

知识点

以下是本文的知识点总结：

知识点	内容概述
计算和电力	计算的本质是加法，电信号的通断可以用于表示二进制的逻辑状态，从而与加法结合，使用门电路实现二进制计算。
门电路	门电路执行基本的逻辑操作（与、或、非），是构建复杂电子系统的基础。二进制加法与形式逻辑的析取操作有相似之处，门电路可以模拟这些逻辑运算。
基本门电路	包括与门（AND）、或门（OR）、非门（NOT），这些电路可以用于实现简单的逻辑运算，二进制加法的基本操作可通过这些门电路实现。
进阶门电路	包括与非门（NAND）、或非门（NOR）、异或门（XOR）、同或门（XNOR），这些门电路通过组合基本逻辑门，实现更复杂的逻辑功能。
真值表	用来描述逻辑门或布尔表达式的工作方式，列出了所有可能的输入组合及对应的输出结果，是理解门电路逻辑运算的工具。
不能进位的门电路计算机	使用或门实现简单的二进制加法器，只能处理没有进位的加法（例如0+0, 0+1, 1+0）。
能进一位的门电路计算机	通过结合XOR和AND逻辑门，处理二进制中1+1=10的加法问题，实现简单的进位运算。
半加器	半加器处理两个二进制数的加法，不考虑低位进位输入，输出一个和位（Sum）和一个进位位（Carry），适用于最基本的加法运算。
全加器	全加器处理二进制数加法，考虑低位进位输入，有三个输入（A、B、Cin）和两个输出（Sum、Cout），能处理多位数的加法，通过门电路组合实现。
门电路实现全加器	使用XOR、AND和OR门电路实现全加器的逻辑运算，Sum通过两个XOR门实现，Cout通过多个AND门和OR门组合实现，保证了加法和进位的正确计算。

这张表格概括了全文的主要知识点，并展示了从计算的基本原理到实现进阶逻辑电路的过程。

结语

祝贺你读完了全文，但是请别忘记这只是个制造计算机的开始，后续还有更多的门电路会引入，作为数字电路基础的一部分。⁴但如果只求原理的读者可以直接跳到LLM部分。
PS:我之所以不直接丢人话解释是因为需要大家真的去思考一下超过自己知识范围的话，然后再结合一些相对好理解到话去领会。说白了就是动点脑子。

---

---

注释：